물리학 초보 필수 유튜브 꿀팁: 그래프로 1차원 운동 문제 해결 방법!
- 가속도-시간 그래프(at 그래프)를 바탕으로 속도-시간 그래프(vt 그래프)와 변위-시간 그래프(st 그래프)를 도출하여 물리 문제를 해결합니다.
- 각 그래프 아래 면적을 통해 구간별 속도 변화량(델타 V)와 변위 변화량(델타 S)을 계산합니다.
- 그래프 분석법을 통해 문제 해결 과정을 단순화하고 시각적으로 이해할 수 있습니다.
물리 문제 해결 노하우: 그래프를 이용한 1차원 운동 분석법
1차원 운동 문제를 풀 때, 특히 가속도가 시간에 따라 변하는 경우에는 그래프를 활용하는 것이 매우 효과적입니다. 주어진 텍스트에서는 가속도-시간 그래프(at 그래프)를 이용하여 속도-시간 그래프(vt 그래프)와 변위-시간 그래프(st 그래프)를 차례대로 도출하고, 이를 통해 문제에서 요구하는 특정 시간에서의 속력과 움직인 거리를 구하는 방법을 자세히 설명하고 있습니다. 이 방법은 복잡한 계산 없이 직관적으로 문제를 해결할 수 있도록 도와줍니다.
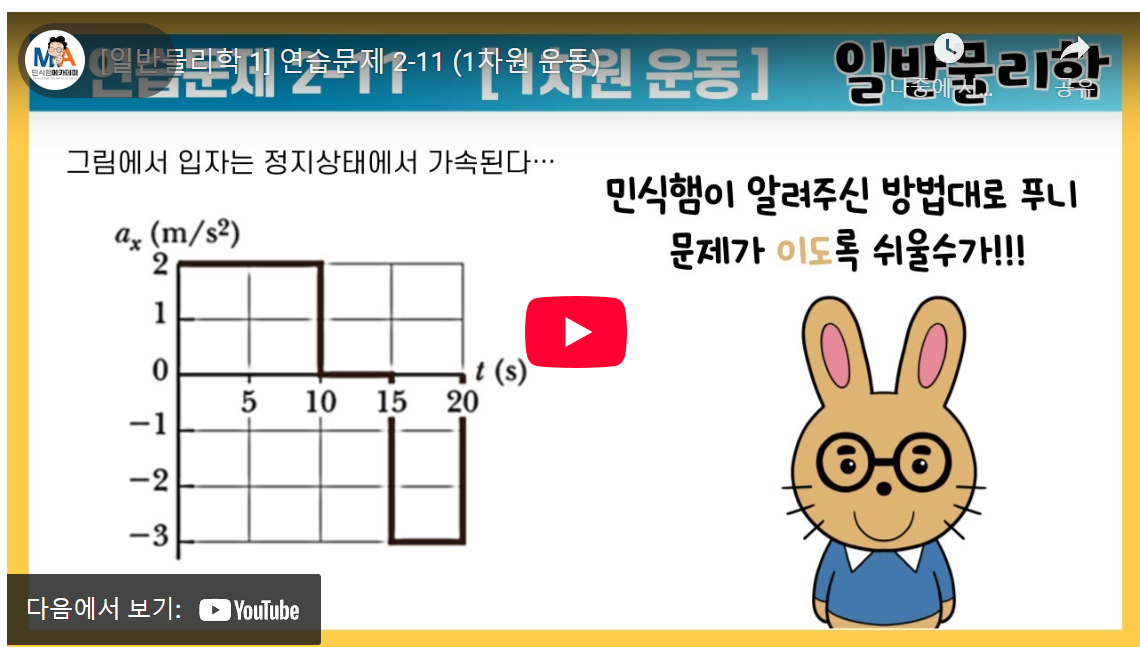
가장 먼저 해야 할 일은 주어진 가속도-시간 그래프(at 그래프)를 분석하는 것입니다. 텍스트 예시에서는 0초에서 10초까지 가속도가 2m/s²으로 일정하고, 10초에서 15초까지는 0m/s², 15초에서 20초까지는 -3m/s²으로 일정한 at 그래프가 제시되었습니다. 이처럼 at 그래프는 시간 구간별로 가속도 변화를 한눈에 보여주기 때문에, 운동 상태를 파악하는 데 매우 유용합니다.
at 그래프를 바탕으로 속도-시간 그래프(vt 그래프)를 그려낼 수 있습니다. vt 그래프에서 각 구간의 속도 변화량(델타 V)은 at 그래프 아래의 면적과 같습니다. 예를 들어, 0초에서 10초 구간에서 at 그래프의 면적은 2m/s² * 10s = 20m/s*이므로, vt 그래프에서 속도는 20m/s만큼 증가합니다. 문제에서 입자가 정지 상태에서 출발했다고 주어졌으므로, 초기 속도는 0m/s입니다. 따라서 10초 후 속도는 0m/s + 20m/s = 20m/s가 됩니다.
10초에서 15초 구간에서는 가속도가 0이므로, vt 그래프의 기울기는 0이 됩니다. 즉, 속도는 변하지 않고 일정하게 유지됩니다. 따라서 이 구간에서는 vt 그래프가 수평선으로 나타나며, 속도는 20m/s로 유지됩니다.
15초에서 20초 구간에서는 가속도가 -3m/s²으로 음수입니다. at 그래프의 면적은 -3m/s² * 5s = -15m/s*이므로, vt 그래프에서 속도는 15m/s만큼 감소합니다. 15초에서의 속도가 20m/s였으므로, 20초 후 속도는 20m/s - 15m/s = 5m/s가 됩니다. 이렇게 각 구간별 속도 변화량을 계산하고, 이전 속도에 더하거나 빼는 방식으로 vt 그래프를 완성할 수 있습니다.
vt 그래프가 완성되면, 변위-시간 그래프(st 그래프)를 그릴 차례입니다. st 그래프에서 각 구간의 변위 변화량(델타 S)은 vt 그래프 아래의 면적과 같습니다. 0초에서 10초 구간에서 vt 그래프는 기울기가 양수인 1차 함수 형태를 띠고, 이를 적분하면 아래로 볼록한 2차 함수 형태의 st 그래프가 됩니다. 이 구간의 변위 변화량은 vt 그래프 아래의 면적을 계산하여 구할 수 있습니다.
10초에서 15초 구간에서 vt 그래프는 상수 함수 형태이므로, st 그래프는 기울기가 양수인 1차 함수 형태가 됩니다. 이 구간의 변위 변화량은 vt 그래프 아래의 면적, 즉 20m/s * 5s = 100m*입니다. 따라서 이 구간 동안 100m를 더 움직이게 됩니다.
15초에서 20초 구간에서 vt 그래프는 기울기가 음수인 1차 함수 형태이므로, st 그래프는 위로 볼록한 2차 함수 형태가 됩니다. 이 구간의 변위 변화량은 사다리꼴 면적을 계산하여 구할 수 있습니다. 텍스트에서는 사다리꼴 면적을 (밑변 + 윗변) / 2 * 높이*공식을 이용하여 62.5m로 계산했습니다. 따라서 이 구간 동안 62.5m를 추가로 움직입니다.
문제에서 10초와 20초에서의 속력을 물었습니다. vt 그래프에서 10초에 해당하는 속도는 20m/s이고, 20초에 해당하는 속도는 5m/s임을 쉽게 확인할 수 있습니다. 또한, 처음 20초 동안 움직인 거리는 st 그래프에서 20초일 때의 변위 값을 통해 알 수 있습니다. 각 구간별 변위 변화량을 모두 더하면 총 움직인 거리를 구할 수 있으며, 텍스트에서는 최종적으로 262.5m를 움직인 것으로 계산되었습니다.
정리하자면, 1차원 운동 문제, 특히 가속도가 변하는 운동의 경우에는 at, vt, st 그래프를 순차적으로 그려서 분석하면 문제를 효과적으로 해결할 수 있습니다. at 그래프에서 vt 그래프를, vt 그래프에서 st 그래프를 도출할 때 각 그래프 아래의 면적이 중요한 역할을 한다는 것을 명심해야 합니다. 이러한 그래프 분석법은 복잡한 운동 상황을 시각적으로 이해하고, 문제 해결 과정을 단순화하는 데 매우 유용합니다.ㅠ
