이미지 생성시 보이는 용어 Fp16, Fp8 차이가 뭘까?

Fp16, Fp8 차이

fp16과 fp8은 부동소수점(floating point) 숫자를 표현하는 데 사용되는 다른 정밀도 형식을 나타냅니다. 이 형식들은 주로 딥러닝 모델, 특히 대규모 언어 모델이나 이미지 생성 모델에서 사용됩니다.

1. fp16 (반정밀도, Half Precision):

   • 16비트를 사용하여 숫자를 표현합니다.

   • 더 넓은 범위의 숫자를 표현할 수 있습니다.

   • fp32(단정밀도)에 비해 메모리 사용량이 절반으로 줄어듭니다.

   • 연산 속도가 더 빠릅니다.

2. fp8 (8비트 부동소수점, 8-bit Floating Point):

   • 8비트만을 사용하여 숫자를 표현합니다.

   • fp16에 비해 표현할 수 있는 숫자의 범위가 더 제한적입니다.

   • 메모리 사용량이 fp16의 절반으로 줄어듭니다.

   • 연산 속도가 더욱 빨라집니다.

주요 차이점:

1. 정밀도: fp16이 fp8보다 더 높은 정밀도를 제공합니다. 즉, fp16은 더 세밀한 숫자 표현이 가능합니다.

2. 메모리 사용: fp8은 fp16에 비해 메모리 사용량이 절반으로 줄어듭니다. 이는 더 큰 모델을 같은 하드웨어에서 실행할 수 있게 해줍니다.

3. 연산 속도: fp8은 일반적으로 fp16보다 더 빠른 연산 속도를 제공합니다.

4. 정확성: fp16이 fp8보다 더 정확한 결과를 제공할 수 있습니다. fp8은 정밀도가 낮아 일부 경우에 정확성이 떨어질 수 있습니다.

5. 적용 범위: fp16은 더 널리 사용되고 지원되는 반면, fp8은 비교적 새로운 형식으로 모든 하드웨어나 프레임워크에서 지원되지 않을 수 있습니다.

이미지 생성 모델의 경우, fp16을 사용하면 좋은 품질의 이미지를 생성하면서도 적당한 속도와 메모리 효율성을 얻을 수 있습니다. fp8은 더 빠른 속도와 낮은 메모리 사용량을 제공하지만, 이미지 품질에 영향을 줄 수 있습니다.

FP (Floating Point) : 부동소수점이라고도 합니다.

1. 정의: 부동소수점은 매우 크거나 매우 작은 숫자를 효율적으로 표현할 수 있는 수 체계입니다. "부동"이란 소수점의 위치가 고정되어 있지 않고 "떠다닌다(float)"는 의미에서 유래했습니다.

2. 구조: 부동소수점 수는 보통 다음 세 부분으로 구성됩니다:

   • 부호(sign): 양수인지 음수인지 나타냅니다.

   • 지수(exponent): 소수점의 위치를 나타냅니다.

   • 가수(mantissa 또는 significand): 실제 숫자의 유효 자릿수를 나타냅니다.

3. 표현 방식: 숫자 = (-1)^부호 × 가수 × 밑수^지수 예를 들어, 2진수 시스템에서 밑수는 2입니다.

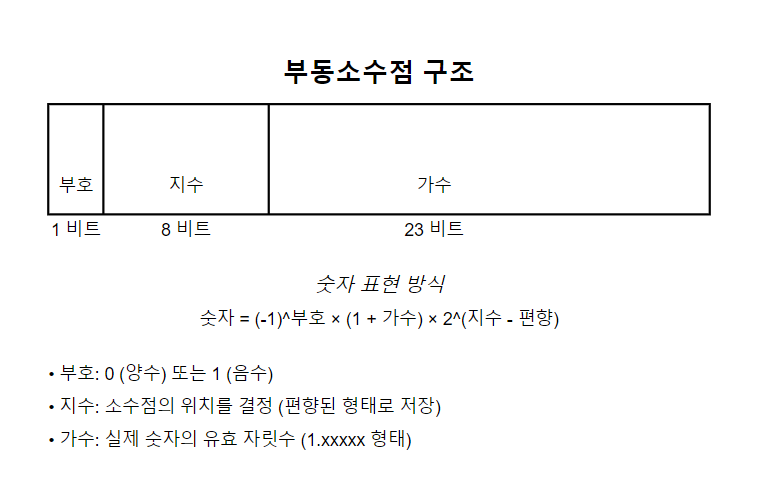
예를 들면, 위의 경우는 32비트의 경우 부동소수점 구조를 보여주고 있습니다.

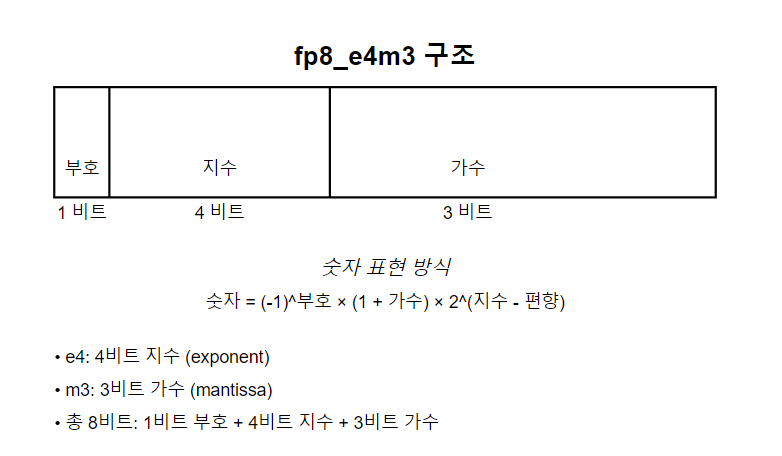
** 이미지 생성시 Clip 모델을 보면 fp8_e4m3 이렇게 표기되는 것이 있는데 , 이는 8비트 경우 1자리는 부호, 지수부는 4 가수부는 3 이런식으로 할당해서 사용한 형식이라고 보시면 될 것 같아요.*

1. 장점:

   • 매우 큰 숫자부터 매우 작은 숫자까지 넓은 범위의 수를 표현할 수 있습니다.

   • 정밀도를 조절할 수 있어 메모리 사용과 계산 속도를 최적화할 수 있습니다.

2. 단점:

   • 정확한 표현이 어려운 경우가 있습니다 (예: 0.1을 정확히 표현하기 어려움).

   • 연산 과정에서 오차가 발생할 수 있습니다.

3. 사용 예:

   • 과학 계산, 3D 그래픽스, 머신러닝 등 정밀한 실수 계산이 필요한 분야에서 널리 사용됩니다.

4. 표준: IEEE 754는 부동소수점 표현의 가장 일반적인 표준으로, 다양한 정밀도(예: 단정밀도 32비트, 배정밀도 64비트)를 정의합니다.

부동소수점은 컴퓨터가 실수를 다루는 데 매우 중요한 개념입니다. 특히 AI와 같은 복잡한 계산을 요구하는 분야에서 정밀도와 효율성의 균형을 맞추는 데 중요한 역할을 합니다.