[쉽게 설명해보기] 베이즈 정리

원리 이해하기

1. 서론: 친근한 비유로 시작하기

• 비유: "쿠키가 사라진 상황"을 예로 들어 베이즈 정리의 기본을 설명합니다.

  • 상황 설정: 부엌에서 쿠키가 사라졌어요. 집에는 엄마, 아빠, 그리고 당신이 있어요.

  • 문제 정의: 쿠키를 누가 먹었을까요?

  • 목표: 쿠키 사건을 통해 베이즈 정리의 기본 원리를 이해해 봅시다.

2. 기본 원리 설명: 쉬운 예시로 접근

• 단계 1: 사전 확률 설명

  • 비유: 아빠는 보통 쿠키를 잘 안 먹어요(20% 확률), 엄마는 가끔 먹어요(30% 확률), 당신은 자주 먹어요(50% 확률).

• 단계 2: 가능성과 증거 추가

  • 증거 추가: 부엌에서 엄마의 목소리가 들렸어요.

  • 가능성 고려: 엄마가 부엌에 있었다는 증거를 어떻게 해석할까요?

• 단계 3: 사후 확률 설명

  • 비유 변경: 증거(엄마의 목소리)를 고려한 후, 쿠키를 누가 먹었을지 확률이 어떻게 바뀌었을까요?

3. 심화 이해: 복잡한 상황 추가

• 상황 추가: 이제, 쿠키 옆에 엄마의 머그컵이 발견되었어요.

• 사후 확률 재조정: 이 새로운 증거는 엄마가 쿠키를 먹었을 확률을 어떻게 바꿀까요?

4. 베이즈 정리의 응용: 다양한 활용 예시 제시

• 응용 1: 날씨 예측 - "비가 올 확률은 어떻게 바뀔까요?"

• 응용 2: 질병 진단 - "어떤 증상이 나타났을 때, 특정 질병에 걸린 확률은?"

• 응용 3: 추천 시스템 - "당신이 이 영화를 좋아할 확률은 얼마나 될까요?"

5. 결론: 일상에서의 활용

• 마무리: 베이즈 정리는 주변에서 일어나는 많은 일들을 이해하고 예측하는 데 도움을 줄 수 있어요. 증거와 정보가 바뀔 때마다 우리의 추측도 업데이트해야 해요.

대화식 설명 전략

각 단계마다 아이의 반응을 확인하며, 이해하지 못한 부분은 더 친절하고 구체적인 예시로 재설명합니다. 예를 들어, 아이가 사후 확률의 개념을 이해하기 어려워한다면, 더 많은 쿠키 예시나 다른 간단한 예(예: 장난감 찾기)를 들어 설명합니다.

이 계획을 통해 아이들은 복잡해 보이는 베이즈 정리를 일상적인 문제 해결에 적용하는 방법을 배우게 됩니다. 중요한 것은 아이들이 재미를 느끼며 자연스럽게 학습하는 것입니다.

쿠키 비유를 활용한 베이즈 정리 교안

1. 서론: 호기심을 자극하기

• 이야기 시작: "어느 날, 부엌에서 맛있는 쿠키가 사라졌어요. 엄마, 아빠, 그리고 당신 중 누가 쿠키를 먹었을까요?"

2. 사전 확률 설명: 배경 지식 소개

• 상황 설명: "아빠는 쿠키를 별로 안 좋아해서, 쿠키를 먹을 확률이 20%예요. 엄마는 가끔 쿠키를 좋아해서, 30% 확률로 쿠키를 먹어요. 그리고 당신은 쿠키를 정말 좋아해서, 50% 확률로 쿠키를 먹지요."

• 도구 사용: 사전 확률을 설명하기 위해 그림이나 색칠 활동을 사용합니다. 각각의 확률을 다른 색으로 표현해봅니다.

3. 증거 추가와 가능성: 증거를 발견하다

• 증거 소개: "그런데 부엌에서 엄마의 머그컵을 발견했어요. 이 증거는 무엇을 의미할까요?"

• 가능성 탐구: "이 증거를 바탕으로, 엄마가 쿠키를 먹었을 가능성이 더 커졌어요. 하지만 아직 확실하지 않아요."

4. 사후 확률 설명: 증거를 바탕으로 추측 업데이트하기

• 사후 확률 도입: "엄마의 머그컵을 발견한 후, 엄마가 쿠키를 먹었을 확률은 어떻게 변했을까요?"

• 활동: 사후 확률을 아이들이 이해할 수 있도록 간단한 게임이나 활동으로 설명합니다. 예를 들어, "머그컵 찾기 게임"을 통해 증거가 확률에 어떻게 영향을 미치는지 보여줍니다.

5. 베이즈 정리 공식 소개: 간단하게 풀어 설명하기

• 공식 소개: "베이즈 정리는 우리가 새로운 증거를 발견할 때마다, 무엇이 진짜일지에 대한 추측을 더 잘 할 수 있게 도와줘요."

• 간단한 설명: "만약 엄마의 머그컵을 더 많이 발견한다면, 엄마가 쿠키를 먹었을 확률은 더 높아져요. 이것이 바로 베이즈 정리가 우리에게 알려주는 거예요."

6. 마무리: 일상 생활로 연결하기

• 일상 생활 예시: "우리는 매일 비슷한 추측을 해요. 예를 들어, 비가 올까 말까 추측할 때도, 비가 오는 증거를 발견할 때마다 우리의 추측을 바꿔요. 이것도 베이즈 정리를 사용하는 거예요."

• 정리: "그래서 베이즈 정리는 우리가 세상을 더 잘 이해하고, 더 좋은 결정을 내리도록 도와준답니다."

활동 제안

• 베이즈 정리 색칠하기: 각 단계별 확률을 다른 색으로 색칠하며, 증거를 추가할 때마다 색칠하는 부분을 바꿔보세요.

• 추측 게임: 다양한 증거(장난감, 책 등)를 바탕으로 무엇이 숨겨져 있을지 추측해보는 게임을 해봅니다.

발렌타인 초콜렛 비유

1. 이유 불충분의 원리 적용

   • 상대방이 나를 좋아할 확률: 50%

   • 상대방이 나를 좋아하지 않을 확률: 50%

2. 조건부 확률 정보 수집

• 좋아하는 사람에게 초콜릿을 줄 확률: 40%

• 호감이 없는 사람에게 예의상 초콜릿을 주는 확률: 30%

3. 상황 가정

• 100명 중 50명은 호감을 얻고 있음

• 100명 중 나머지 50명은 호감을 얻고 있지 않음

4. 호감 있는 경우

• 초콜릿을 받을 확률: 20명 (40%)

• 초콜릿을 받지 않을 확률: 30명 (60%)

5. 호감 없는 경우

   • 예의상 초콜릿을 받을 확률: 15명 (30%)

   • 초콜릿을 받지 않을 확률: 35명 (70%)

6. 초콜릿을 받았을 때 호감 있는 확률 계산

• 초콜릿을 받은 총 사람 수: 35명 (20명의 호감 + 15명의 예의상)

• 초콜릿을 받았을 때, 호감이 있는 사람의 비율: ( frac{20}{35} = 57% )

7. 결론

   • 초콜릿을 받음으로써 상대방이 나에게 호감을 가질 확률: 사전확률 50%에서 사후확률 57%로 상승

   • 이 과정을 통해 베이즈 정리 적용

8. 베이즈 정리의 핵심

• 사전확률: 상대방이 나를 좋아할 초기 확률 50%

• 사후확률: 새로운 정보(초콜릿을 받음)를 바탕으로 업데이트된 확률 57%

9. 상황 시각화

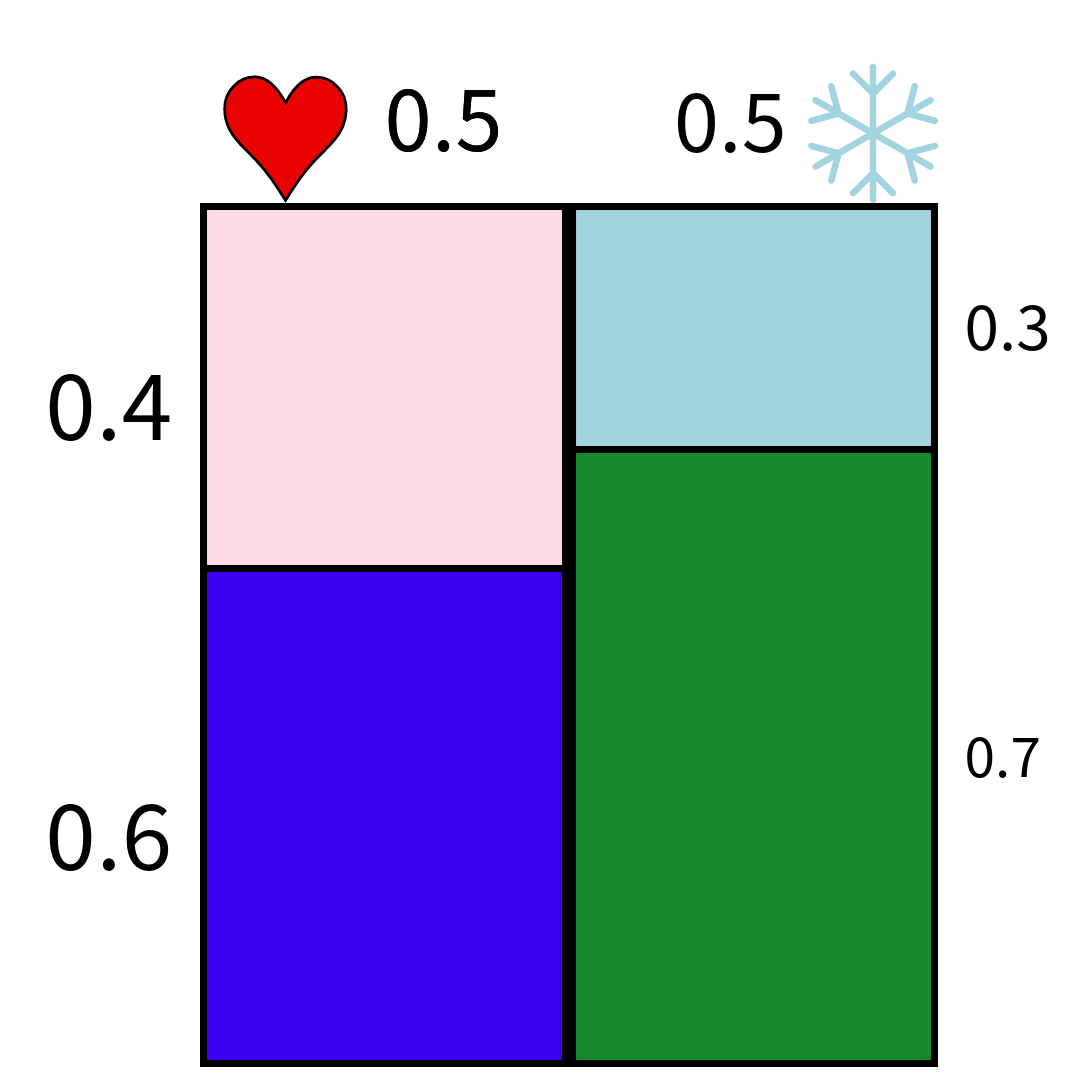
   • 사각형 전체 면적을 1이라 가정 (전체 확률 100%)

   • 가로 길이: 상대방이 나를 좋아하거나 좋아하지 않을 확률 (각각 0.5)

   • 세로 길이: 초콜릿을 줄 확률

     • 좋아할 때: 40% (0.4)

     • 좋아하지 않을 때: 30% (0.3)

   • 사각형 분할: 호감 있을 때/없을 때, 초콜릿을 줄/주지 않을 확률로 구분

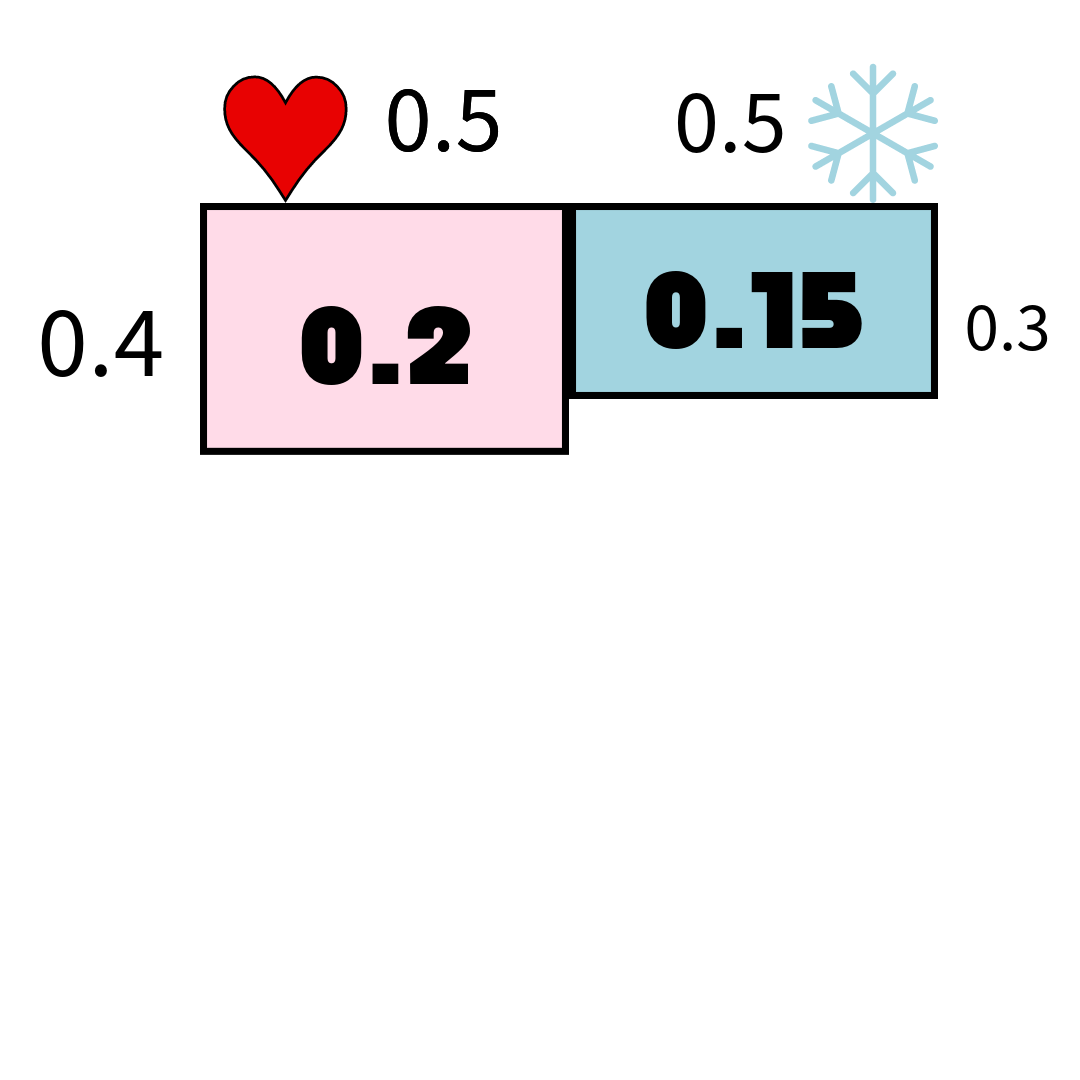
10. 초콜릿을 받았을 때의 확률 재계산

• 초콜릿을 받은 영역: 좋아하면서 초콜릿을 준 경우와 예의상 준 경우의 합

• 사후확률 계산: ( frac{호감 있으면서 초콜릿을 받은 영역}{초콜릿을 받은 총 영역} = 57% )

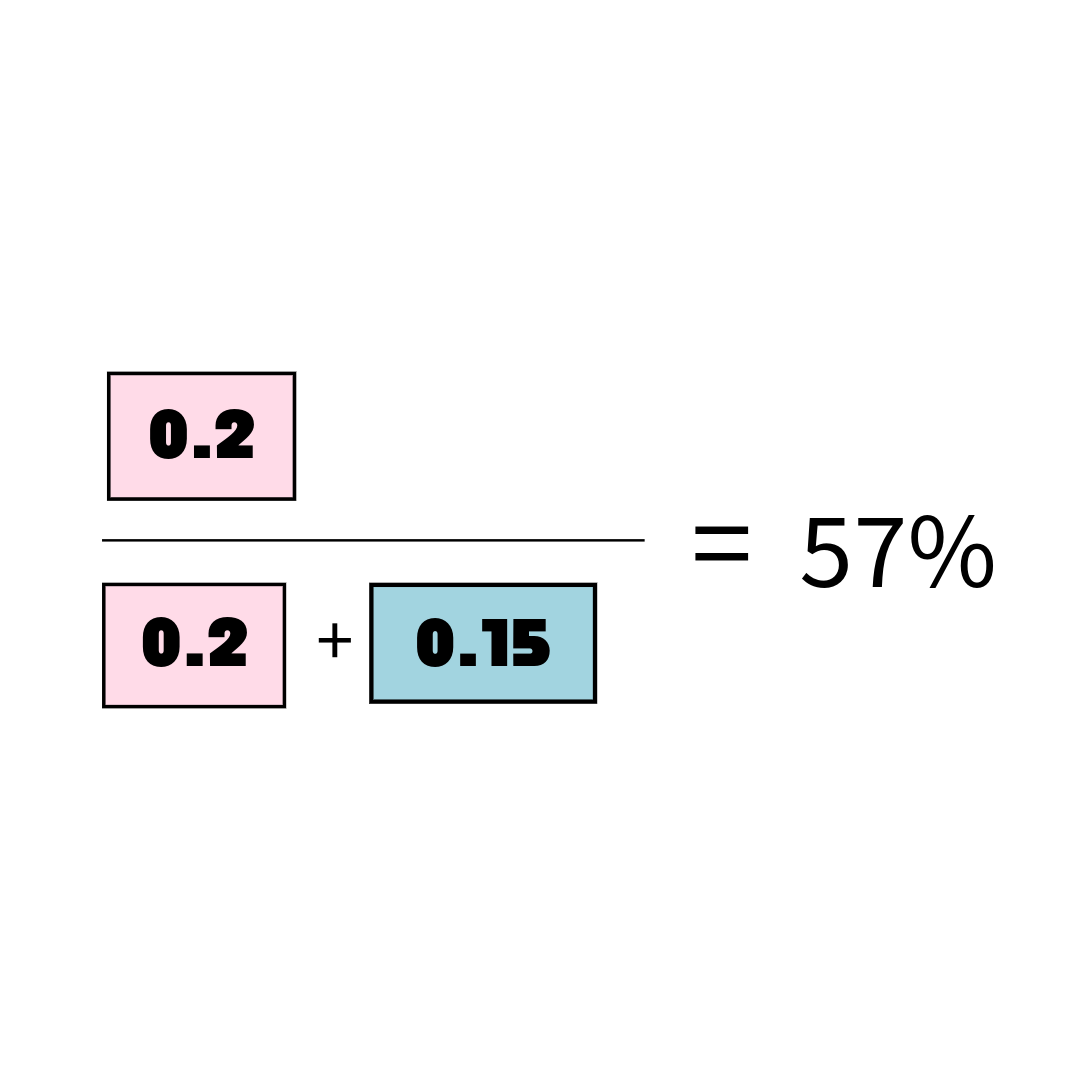
** 사전확률로 사후확률을 얻는 것

11. 베이즈 정리의 응용

• 사전확률을 바탕으로 새로운 정보를 통해 사후확률을 업데이트

• 데이터가 많아질수록 더 정확한 의사결정 가능

12. 결론 도출

• 베이즈 정리는 의사결정 과정에서 매우 중요

• 현대에서는 인공지능 의사결정에도 중요한 역할을 함

• 실생활에서의 의사결정, 경영학의 '린 방식' 등에도 적용됨